TL-B 타입
이 정보는 매우 저수준이며 초보자가 이해하기 어려울 수 있습니다. 나중에 읽어도 괜찮습니다.
이 섹션에서는 복잡하고 특이한 타입 언어 바이너리(TL-B) 구조를 분석합니다. 시작하기 전에 주제에 더 익숙해지기 위해 이 문서를 먼저 읽어보는 것을 권장합니다.

Either
left$0 {X:Type} {Y:Type} value:X = Either X Y;
right$1 {X:Type} {Y:Type} value:Y = Either X Y;
Either 타입은 두 가지 결과 타입 중 하나가 가능할 때 사용됩니다. 이 경우 타입 선택은 표시된 접두사 비트에 따라 달라집니다. 접두사 비트가 0이면 왼쪽 타입이 직렬화되고, 1 접두사 비트가 사용되면 오른쪽 타입이 직렬화됩니다.
예를 들어 메시지를 직렬화할 때, 본문이 메인 셀의 일부이거나 다른 셀에 연결될 때 사용됩니다.
Maybe
nothing$0 {X:Type} = Maybe X;
just$1 {X:Type} value:X = Maybe X;
Maybe 타입은 선택적 값과 함께 사용됩니다. 이러한 경우 첫 번째 비트가 0이면 값 자체가 직렬화되지 않고(실제로 건너뜀) 값이 1이면 직��렬화됩니다.
Both
pair$_ {X:Type} {Y:Type} first:X second:Y = Both X Y;
Both 타입 변형은 일반 쌍과 함께만 사용되며, 두 타입이 조건 없이 하나씩 차례로 직렬화됩니다.
Unary
Unary 함수 타입은 hml_short와 같은 구조에서 동적 크기 조정에 일반적으로 사용됩니다.
Unary는 두 가지 주요 옵션을 제공합니다:
unary_zero$0 = Unary ~0;
unary_succ$1 {n:#} x:(Unary ~n) = Unary ~(n + 1);
Unary 직렬화
일반적으로 unary_zero 변형의 사용은 매우 간단합니다: 첫 번째 비트가 0이면 전체 Unary 역직렬화의 결과는 0입니다.
그러나 unary_succ 변형은 재귀적으로 로드되고 ~(n + 1)의 값을 가지기 때문에 더 복잡합니다. 이는 unary_zero에 도달할 때까지 순차적으로 자신을 호출합니다. 다시 말해, 원하는 값은 연속된 단위의 수와 같습니다.
예를 들어, 비트열 110의 직렬화를 분석해보겠습니다.
호출 체인은 다음과 같습니다:
unary_succ$1 -> unary_succ$1 -> unary_zero$0
unary_zero에 도달하면 값은 재귀 함수 호출처럼 직렬화된 비트열의 끝으로 반환됩니다.
이제 결과를 더 명확하게 이해하기 위해 반환 값 경로를 가져와보면 다음과 같이 표시됩니다:
0 -> ~(0 + 1) -> ~(1 + 1) -> 2, 이는 우리가 110을 Unary 2로 직렬화했음을 의미합니다.
Unary 역직렬화
Foo 타입이 있다고 가정해봅시다:
foo$_ u:(Unary 2) = Foo;
위에서 말한 바와 같이, Foo는 다음과 같이 역직렬화됩니다:
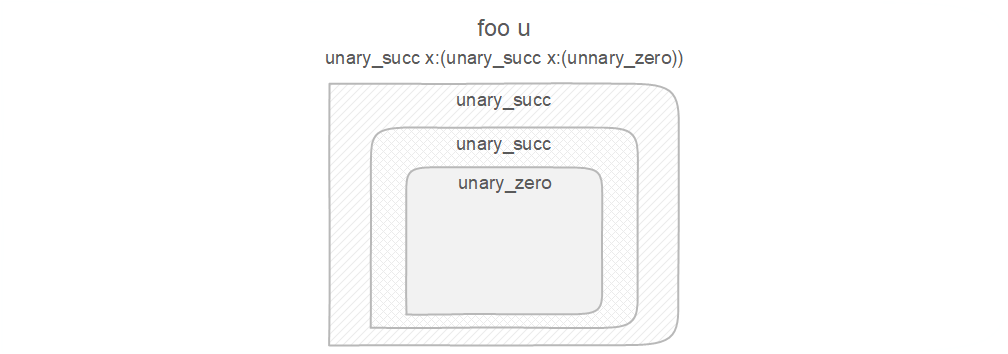
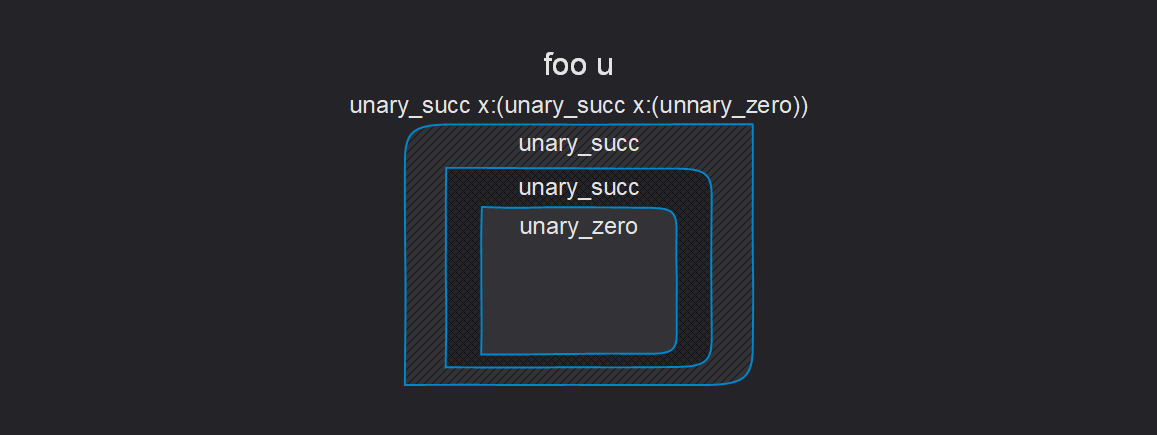
foo u:(unary_succ x:(unary_succ x:(unnary_zero)))
Hashmap
Hashmap 복합 타입은 FunC 스마트 계약 코드(dict)의 dict를 저장하는 데 사용됩니다.
다음 TL-B 구조는 고정 키 길이를 가진 Hashmap을 직렬화하는 데 사용됩니다:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(HashmapNode m X) = Hashmap n X;
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
hmn_fork#_ {n:#} {X:Type} left:^(Hashmap n X)
right:^(Hashmap n X) = HashmapNode (n + 1) X;
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= m} s:(n * Bit) = HmLabel ~n m;
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
hml_same$11 {m:#} v:Bit n:(#<= m) = HmLabel ~n m;
unary_zero$0 = Unary ~0;
unary_succ$1 {n:#} x:(Unary ~n) = Unary ~(n + 1);
hme_empty$0 {n:#} {X:Type} = HashmapE n X;
hme_root$1 {n:#} {X:Type} root:^(Hashmap n X) = HashmapE n X;
이는 루트 구조가 HashmapE와 hme_empty 또는 hme_root 두 상태 중 하나를 사용한다는 것을 의미합니다.
Hashmap 파싱 예제
예를 들어 이진 형식으로 주어진 다음 Cell을 고려해보겠습니다.
1[1] -> {
2[00] -> {
7[1001000] -> {
25[1010000010000001100001001],
25[1010000010000000001101111]
},
28[1011100000000000001100001001]
}
}
이 Cell은 HashmapE 구조 타입을 �사용하고 8비트 키 크기를 가지며 값은 uint16 숫자 프레임워크를 사용합니다(HashmapE 8 uint16). HashmapE는 3가지 고유한 키 타입을 사용합니다:
1 = 777
17 = 111
128 = 777
이 Hashmap을 파싱하기 위해서는 어떤 구조 타입을 사용할지, hme_empty나 hme_root 중 어떤 것을 사용할지 미리 알아야 합니다. 이는 올바른 접두사를 식별하여 결정됩니다. hme empty 변형은 1비트 0(hme_empty$0)을 사용하고, hme root는 1비트 1(hme_root$1)을 사용합니다. 첫 번째 비트를 읽은 후, 그것이 1(1[1])과 같다는 것을 확인하면 이는 hme_root 변형임을 의미합니다.
이제 알려진 값으로 구조 변수를 채��워보면 초기 결과는 다음과 같습니다:
hme_root$1 {n:#} {X:Type} root:^(Hashmap 8 uint16) = HashmapE 8 uint16;
여기서 1비트 접두사는 이미 읽었지만, {}안에 있는 것은 읽을 필요가 없는 조건들입니다. 조건 {n:#}는 n이 uint32 숫자이고, {X:Type}는 X가 어떤 타입이든 사용할 수 있음을 의미합니다.
다음으로 읽어야 할 부분은 root:^(Hashmap 8 uint16)이며, ^ 기호는 로드해야 하는 링크를 나타냅니다.
2[00] -> {
7[1001000] -> {
25[1010000010000001100001001],
25[1010000010000000001101111]
},
28[1011100000000000001100001001]
}
브랜치 파싱 시작
우리의 스키마에 따르면, 이것은 올바른 Hashmap 8 uint16 구조입니다. 다음으로 알려진 값으로 채우면 다음과 같은 결과를 얻습니다:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l 8)
{8 = (~m) + l} node:(HashmapNode m uint16) = Hashmap 8 uint16;
위에서 볼 수 있듯이, 조건 변수 {l:#}와 {m:#}가 나타났지만, 두 변수의 값은 알 수 없습니다. 또한, 해당 label을 읽은 후, n이 방정식 {n = (~m) + l}에 관여한다는 것이 분명해지며, 이 경우 l과 m을 계산하고, ~ 기호는 결과 값을 알려줍니다.
l의 값을 결정하기 위해서는 label:(HmLabel ~l uint16) 시퀀스를 로드해야 합니다. 아래에서 볼 수 있듯이, HmLabel은 3가지 기본 구조 옵션을 가집니다:
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= m} s:(n * Bit) = HmLabel ~n m;
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
hml_same$11 {m:#} v:Bit n:(#<= m) = HmLabel ~n m;
각 옵션은 해당하는 접두사로 결정됩니다. 현재 우리의 루트 셀은 2개의 0비트로 구성되어 있으며(2[00]), 따라서 유일한 논리적 옵션은 0으로 시작하는 접두사를 사용하는 hml_short$0입니다.
hml_short에 알려진 값을 채웁니다:
hml_short$0 {m:#} {n:#} len:(Unary ~n) {n <= 8} s:(n * Bit) = HmLabel ~n 8
이 경우 n의 값을 모르지만, ~ 문자가 있기 때문에 계산할 수 있습니다. 이를 위해 len:(Unary ~n)을 로드합니다(Unary에 대해 자세히 보기).
이 경우 2[00]로 시작했지만, HmLabel 타입을 정의한 후에는 두 비트 중 하나만 남아있습니다.
따라서 이를 로드하면 값이 0임을 알 수 있고, 이는 분명히 unary_zero$0 변형을 사용한다는 것을 의미합니다. 이는 HmLabel 변형을 사용하는 n 값이 0이라는 것을 의미합니다.
다음으로 계산된 n 값을 사용하여 hml_short 변형 시퀀스를 완성해야 합니다:
hml_short$0 {m:#} {n:#} len:0 {n <= 8} s:(0 * Bit) = HmLabel 0 8
결과적으로 s = 0인 빈 HmLabel이 나오므로, 다운로드할 것이 없습니다.
다음으로 계산된 l 값으로 구조를 보완합니다:
hm_edge#_ {n:#} {X:Type} {l:0} {m:#} label:(HmLabel 0 8)
{8 = (~m) + 0} node:(HashmapNode m uint16) = Hashmap 8 uint16;
이제 l의 값을 계산했으므로, 방정식 n = (~m) + 0, 즉 m = n - 0, m = n = 8을 사용하여 m도 계산할 수 있습니다.
모든 알 수 없는 값을 결정한 후 이제 node:(HashmapNode 8 uint16)를 로드할 수 있습니다.
HashmapNode의 경우, 다음과 같은 옵션이 있습니다:
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
hmn_fork#_ {n:#} {X:Type} left:^(Hashmap n X)
right:^(Hashmap n X) = HashmapNode (n + 1) X;
이 경우 접두사가 아닌 매개변수를 사용하여 옵션을 결정합니다. 이는 n = 0이면 최종 결과가 hmn_leaf 또는 hmn_fork가 될 것임을 의미합니다.
이 예제에서 결과는 n = 8(hmn_fork 변형)입니다. hmn_fork 변형을 사용하고 알려진 값을 채웁니다:
hmn_fork#_ {n:#} {X:uint16} left:^(Hashmap n uint16)
right:^(Hashmap n uint16) = HashmapNode (n + 1) uint16;
알려진 값을 입력한 후, HashmapNode (n + 1) uint16를 계산해야 합니다. 이는 n의 결과 값이 우리의 매개변수와 같아야 함을 의미합니다(즉, 8).
로컬 n 값을 계산하기 위해서는 다음 공식을 사용해야 합니다: n = (n_local + 1) -> n_local = (n - 1) -> n_local = (8 - 1) -> n_local = 7.
hmn_fork#_ {n:#} {X:uint16} left:^(Hashmap 7 uint16)
right:^(Hashmap 7 uint16) = HashmapNode (7 + 1) uint16;
이제 위의 공식이 필요하다는 것을 알았으므로, 최종 결과를 얻는 것은 간단합니다. 다음으로 왼쪽과 오른쪽 브랜치를 로드하고 각 후속 브랜치에 대해 이 과정을 반복합니다.
로드된 Hashmap 값 분석
이전 예제를 계속 이어서, 브랜치 로딩 과정이 어떻게 작동하는지 살펴보겠습니다(dict 값의 경우), 즉 28[1011100000000000001100001001]
최종 결과는 다시 한 번 hm_edge가 되고 다음 단계는 올바른 알려진 값으로 시퀀스를 채우는 것입니다:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l 7)
{7 = (~m) + l} node:(HashmapNode m uint16) = Hashmap 7 uint16;
다음으로 접두사가 10이므로 HmLabel 변형을 사용하여 HmLabel 응답을 로드합니다.
hml_long$10 {m:#} n:(#<= m) s:(n * Bit) = HmLabel ~n m;
이제 시퀀스를 채웁니다:
hml_long$10 {m:#} n:(#<= 7) s:(n * Bit) = HmLabel ~n 7;
새로운 구성 - n:(#<= 7)은 분명히 숫자 7에 해당하는 크기 값을 나타내며, 이는 실제로 숫자의 log2 + 1입니다. 하지만 간단히 하기 위해 숫자 7을 쓰는 데 필요한 비트 수를 세어볼 수 있습니다.
관련하여 이진 형식의 숫자 7은 111입니다. 따라서 3비트가 필요하며, 이는 n = 3이라는 것을 의미합니다.
hml_long$10 {m:#} n:(## 3) s:(n * Bit) = HmLabel ~n 7;
다음으로 시퀀스에 n을 로드하면 결과는 111이 되고, 위에서 언급했듯이 = 7입니다. 다음으로 시퀀스에 s를 로드하면 7비트 - 0000000이 됩니다. s는 키의 일부라는 것을 기억하세요.
다음으로 시퀀스의 맨 위로 돌아가서 결과 l을 채웁니다:
hm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel 7 7)
{7 = (~m) + 7} node:(HashmapNode m uint16) = Hashmap 7 uint16;
그런 다음 m의 값을 계산합니다, m = 7 - 7, 따라서 m = 0입니다.
m = 0이므로, 구조는 HashmapNode와 함께 사용하기에 완벽합니다:
hmn_leaf#_ {X:Type} value:X = HashmapNode 0 X;
다음으로 uint16 타입을 대체하고 값을 로드합니다. 남은 16비트 0000001100001001는 10진수로 777입니다.
이제 키를 복원해보겠습니다. 이전에 계산된 키의 모든 부분을 순서대로 결합해야 합니다. 두 관련 키 부분은 어떤 타입의 브랜치가 사용되는지에 따라 하나의 비트로 결합됩니다. 오른쪽 브랜치의 경우 '1' 비트가 추가되고, 왼쪽 브랜치의 경우 '0' �비트가 추가됩니다. 전체 HmLabel이 위에 있으면 해당 비트가 키에 추가됩니다.
이 경우 특별히, HmLabel에서 7비트 0000000을 가져오고 값이 오른쪽 브랜치에서 얻어졌기 때문에 0의 시퀀스 앞에 '1' 비트를 추가합니다. 최종 결과는 총 8비트 또는 10000000이 되어 키 값은 128이 됩니다.
기타 Hashmap 타입
이제 Hashmap과 표준화된 Hashmap 타입을 로드하는 방법에 대해 논의했으므로, 추가 Hashmap 타입이 어떻게 작동하는지 설명하겠습니다.
HashmapAugE
ahm_edge#_ {n:#} {X:Type} {Y:Type} {l:#} {m:#}
label:(HmLabel ~l n) {n = (~m) + l}
node:(HashmapAugNode m X Y) = HashmapAug n X Y;
ahmn_leaf#_ {X:Type} {Y:Type} extra:Y value:X = HashmapAugNode 0 X Y;
ahmn_fork#_ {n:#} {X:Type} {Y:Type} left:^(HashmapAug n X Y)
right:^(HashmapAug n X Y) extra:Y = HashmapAugNode (n + 1) X Y;
ahme_empty$0 {n:#} {X:Type} {Y:Type} extra:Y
= HashmapAugE n X Y;
ahme_root$1 {n:#} {X:Type} {Y:Type} root:^(HashmapAug n X Y)
extra:Y = HashmapAugE n X Y;
HashmapAugE와 일반 Hashmap의 주요 차이점은 각 노드(값이 있는 리프뿐만 아니라)에 extra:Y 필드가 있다는 것입니다.
PfxHashmap
phm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(PfxHashmapNode m X)
= PfxHashmap n X;
phmn_leaf$0 {n:#} {X:Type} value:X = PfxHashmapNode n X;
phmn_fork$1 {n:#} {X:Type} left:^(PfxHashmap n X)
right:^(PfxHashmap n X) = PfxHashmapNode (n + 1) X;
phme_empty$0 {n:#} {X:Type} = PfxHashmapE n X;
phme_root$1 {n:#} {X:Type} root:^(PfxHashmap n X)
= PfxHashmapE n X;
PfxHashmap과 일반 Hashmap의 주요 차이점은 phmn_leaf$0와 phmn_fork$1 노드가 있어서 서로 다른 키 길이를 저장할 수 있다는 것입니다.
VarHashmap
vhm_edge#_ {n:#} {X:Type} {l:#} {m:#} label:(HmLabel ~l n)
{n = (~m) + l} node:(VarHashmapNode m X)
= VarHashmap n X;
vhmn_leaf$00 {n:#} {X:Type} value:X = VarHashmapNode n X;
vhmn_fork$01 {n:#} {X:Type} left:^(VarHashmap n X)
right:^(VarHashmap n X) value:(Maybe X)
= VarHashmapNode (n + 1) X;
vhmn_cont$1 {n:#} {X:Type} branch:Bit child:^(VarHashmap n X)
value:X = VarHashmapNode (n + 1) X;
// nothing$0 {X:Type} = Maybe X;
// just$1 {X:Type} value:X = Maybe X;
vhme_empty$0 {n:#} {X:Type} = VarHashmapE n X;
vhme_root$1 {n:#} {X:Type} root:^(VarHashmap n X)
= VarHashmapE n X;
VarHashmap과 일반 Hashmap의 주요 차이점은 vhmn_leaf$00와 vhmn_fork$01 노드가 있어서 서로 다른 키 길이를 저장할 수 있다는 것입니다. 또한, VarHashmap은 vhmn_cont$1을 통해 공통 값 접두사(자식 맵)를 형성할 수 있습니다.
BinTree
bta_leaf$0 {X:Type} {Y:Type} extra:Y leaf:X = BinTreeAug X Y;
bta_fork$1 {X:Type} {Y:Type} left:^(BinTreeAug X Y)
right:^(BinTreeAug X Y) extra:Y = BinTreeAug X Y;
이진 트리 키 생성 메커니즘은 표준화된 Hashmap 프레임워크와 유사한 방식으로 작동하지만 레이블을 사용하지 않고 브랜치 접두사만 포함합니다.
주소
TON 주소는 TL-B StateInit 구조를 사용하여 sha256 해싱 메커니즘으로 형성됩니다. 이는 네트워크 계약 배포 전에 주소를 계산할 수 있다는 것을 의미합니다.
직렬화
EQBL2_3lMiyywU17g-or8N7v9hDmPCpttzBPE2isF2GTzpK4와 같은 표준 주소는 바이트 인코딩에 base64 uri를 사용합니다.
일반적으로 36바이트의 길이를 가지며, 마지막 2바이트는 XMODEM 테이블로 계산된 crc16 체크섬이고, 첫 번째 바이트는 플래그를, 두 번째 바이트는 워크체인을 나타냅니다.
중간의 32바이트는 주소 자체의 데이터(AccountID라고도 함)이며, 종종 int256과 같은 스키마로 표현됩니다.
참고
Oleg Baranov의 원본 글 링크입니다.